In addition to isothermal intercritical annealing discussed above, the study of cyclic α→γ and γ→α transformations in the intercritical range is a good method to investigate the growth kinetics in medium-Mn steels. There are certain advantages in studying cyclic phase transformations. The first is that growth can be isolated and studied exclusively without the intervention of nucleation. The second stems from the fact that α→γ and γ→α transformations proceed at different rates isothermally, and, therefore, cyclic transformations can provide insight in the growth kinetics. The cyclic transformations were studied in a Fe-0.2C-5Mn steel (Sarafoglou et al. 2015). The cyclic thermal treatment considered is depicted in Figure 1a. The cycle starts with an isothermal holding at T_is=675^oC followed by temperature cycling between T_max=710^oC and T_min=640^oC. The heating and cooling rates were 10^oC/min. It is important to note that the time were the cyclic transformations starts is important, since the cyclic transformations depend on the previous conditions established during isothermal holding at T_is. Therefore, isothermal intercritical annealing was simulated first and then the start of the cyclic transformations was chosen accordingly. The isothermal α→γ and γ→α transformations are depicted in Figure 1b. Compared with the α→γ, the γ→α transformation is much slower. Two specific times, t_s, were identified as the start of the cyclic transformations. In the first case t_s=1x10⁸ sec after equilibrium volume fractions for both austenite and ferrite have been established in the isothermal transformation. In the second case, ts=2x103 sec, where the α→γ transformation is evolving while the γ→α transformation is very sluggish. These times are depicted by dotted lines in Figure 2b. The cyclic transformations are depicted in Figure 2a and 2b for the times t_s=1x10⁸ sec and t_s=2x10³ sec respectively. In Figure 2a the volume fraction forms hysteresis loops. Point A marks the beginning and point B the end of the cyclic transformation. The loops move upwards indicating that more austenite forms at every cycle. An additional feature of the cyclic behavior is the “inverse” transformation, where the transformation proceeds to a direction opposite to the temperature change. This behavior is depicted by CD for T_max and EF for T_min in Figure 2a. The cyclic transformation for t_s=2x10³ sec is depicted in Figure 2b. Since in this case at t_s=2x10³ sec, the γ→α transformation during the isothermal treatment (Fig.2b) is sluggish, the volume fraction during cyclic transformation does not form hysteresis loops. On the contrary the volume fraction increases in each cycle, both in the heating and cooling part. In this case austenite forms by inverse transformation during the cooling part of the cycle.

Contributors: P.I. Sarafoglou, M.I.T. Tzini and G.N. Haidemenopoulos

Reference: P.I. Sarafoglou, M.I.T. Tzini and G.N. Haidemenopoulos, Simulation of cyclic transformations in the intercritical range of a 5Mn steel, Int. Journal of Materials and Metallurgical Engineering, May 2015, DOI: 10.15344/ijmme/2015/104.

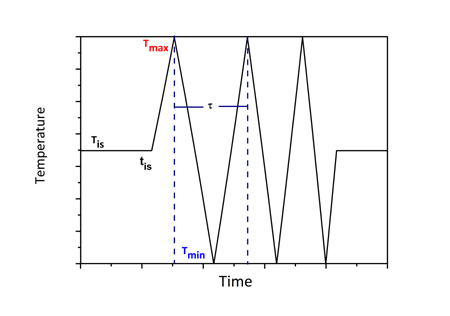Figure 1a: Cyclic thermal treatment.	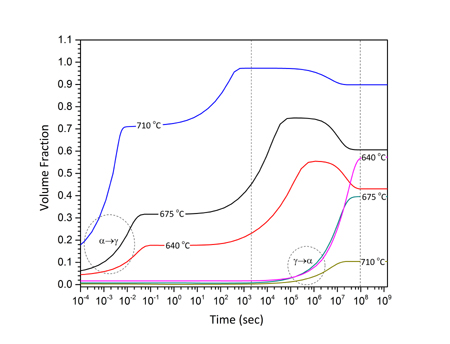Figure 1b: Isothermal volume fractions for the  α→γ and γ→α transformations.
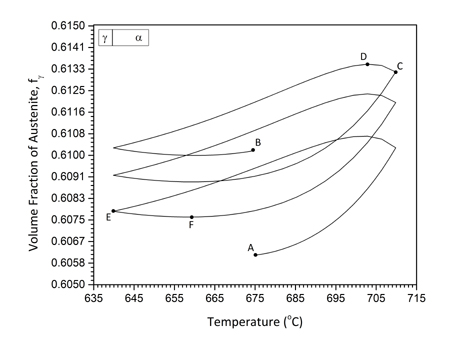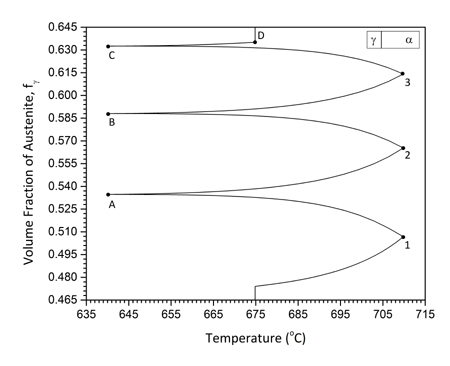Figure 2a:Volume fraction of austenite vs temperature for the α→γ cyclic transformation at ts=2x103 sec.	Figure 2b:Volume fraction of austenite vs temperature for the α→γ cyclic transformation at ts=1x108 sec.